Traveller ist (verglichen mti Fate, Cypher System o.Ä.) relativ realistisch. [...]
An der Stelle der kurze Einwurf, dass Fate eines der Systeme ist, bei der ich endlich mal keine Probleme mit der miesen Physiksimulation habe - weil es keine Physiksimulation gibt. Narrative Systeme sagen: "Es gibt ein Problem, erkläre doch selbst welches." Das klappt zugegebenermaßen besser - und ist auch wahrscheinlich nur dann eine Option - mit einem Physicist in Residence, der dann eine Palette an möglichen Problemen runter rattert, von denen das sinnvollste als Aspekt auf den Tisch gelegt wird (wobei ich mit Physiker auch durchaus Nichtphysiker mit ausreichend Interesse am Thema mit einschließe, z.B. alle KSP-Spieler, die es auch mal ohne Mechjeb zu einem anderen Himmelskörper geschafft haben

). Systeme mit Regeln, um so etwas im Spiel zu simulieren, sorgen bei mir immer ganz schnell dazu, dass ich den Taschenrechner zücke und Schimpfwörter vor mich hin murmle.

Aber zurück zum Thema:
Ist Treibstoff eigentlich ein Problem für die Manövertriebwerke? Wenn ich mich recht erinnere, benutzen die Schiffe bei Traveller doch wahlweise ein Gravitationstriebwerk (puh, wenigstens gibt es mit dem Stern oder anderen schweren Objekten in der Nähe einen Wechselwirkungspartner) oder einen dubiosen
Thruster (jedes einzelne Experiment in der gesamten Geschichte der Naturwissenschaften sagt: Nein! NEIN!!! NIEMALS!!!). Beide bekommen reichlich Energie aus dem Fusionsreaktor, der nach den Büchern eigentlich immer genug Treibstoff hat. Spritfresser ist immer das Sprungtriebwerk. Die langsamen Dinger machen kontinuierlich 1 G.
Damit ist das Sonnensystem dein Spielplatz, weil du richtig schnell ohne Aufwand zwischen den inneren Planeten hin und her schippern kannst. Auch die Gasriesen außerhalb sind keine Woche weit weg. Wenn ich mal ganz grob von einer geradlinigen Bahn ausgehe, dann lande ich bei einem G Beschleunigung von der Erde zum Jupiter heute bei etwas über einer Woche inklusive Angleichung der Bahngeschwindigkeit, die dabei ein bisschen mehr als eine Stunde ausmacht...
1Dann nimmst du jetzt noch die
Universe Sandbox, baust dein Sonnensystem, schiebst die Zeit so weit, wie du sie brauchst, berechnest mit all den lustigen Näherungen aus der Fußnote (*hust*) die Reisezeit mit dieser Gleichung
2 und fertig:
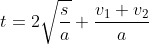
t: Reisezeit in Sekunden
s: Abstand in Metern
a: Beschleunigung des Schiffs, 1G entspricht ca. 10ms
-2v
1, v
2: Bahngeschwindigkeiten der Planeten in m/s
1) Wirklich WIRKLICH WIRKLICH grob angenähert. Distanz von ca. 6,1 AU im Moment. Geradlinige, gleichmäßig beschleunigte Bewegung, auf der Mitte umdrehen und Geschwindigkeit wieder abbauen. Die Anpassung der Relativgeschwindigkeit ist bei schlimmstmöglichem Fall mit (13 kms-1 + 30 kms-1) / 10ms-2 unter anderthalb Stunden erledigt... Das wird eine Abschätzung nach oben sein, die tatsächliche Zeit wird geringer ausfallen, wenn ich mich an der richtigen Stelle aus der Umlaufbahn der Erde raus und beim Jupiter in den Orbit wieder rein beschleunige, schließlich sind die Orbitalgeschwindigkeiten da nicht klein gegenüber den Relativgeschwindigkeiten der beiden Planeten. Egal, wird vernachlässigt. In vier Tagen bewegen sich Planeten nicht weit (ok, absolut aus unserer Sicht schon, relativ zu den Abmessungen eines Sonnensystems? Pffft.) Wird auch vernachlässigt. Und auch die Auswirkung der Gravitationsfelder der Planeten und der Sonne habe ich mal ganz dezent ignoriert, denn die ja nun das eigentlich Problem beim Rechnen.
2) Das hat sooo unendlich keinen Anspruch auf Richtigkeit. Aber als Abschätzung ist das wahrscheinlich nicht abgrundtief schlecht. Für große3, konstante Werte von g und kontinuierlich laufende Triebwerke wird es von der Zehnerpotenz her passabel sein. Und es enthält viele Buchstaben und eine Wurzel. Das fühlt sich supernaturwissenschaftlich an. 
3) 1 G halte ich dabei für groß. Nicht groß wäre das hier.
