Sei n die Zahl der Würfel und k die Zahl der benötigten Erfolge. Mangels besserer Darstellung im Forum notieren wir den Binomialkoeffizienten mit [n;k] = n! / (n-k)! * k!. Dann gilt:
- Die Wahrscheinlichkeit, mit n Würfeln genau k Erfolge zu erzielen, beträgt [n;k] * (0,5)^n.
- Die (für uns interessantere) Wahrscheinlichkeit, mit n Würfeln mindestens k Erfolge zu erzielen, beträgt Summe(i=k..n) [n;k] * (0,5)^n.
Ich habe das mal als Graph gebastelt, einmal für n=10 und einmal für n=9:
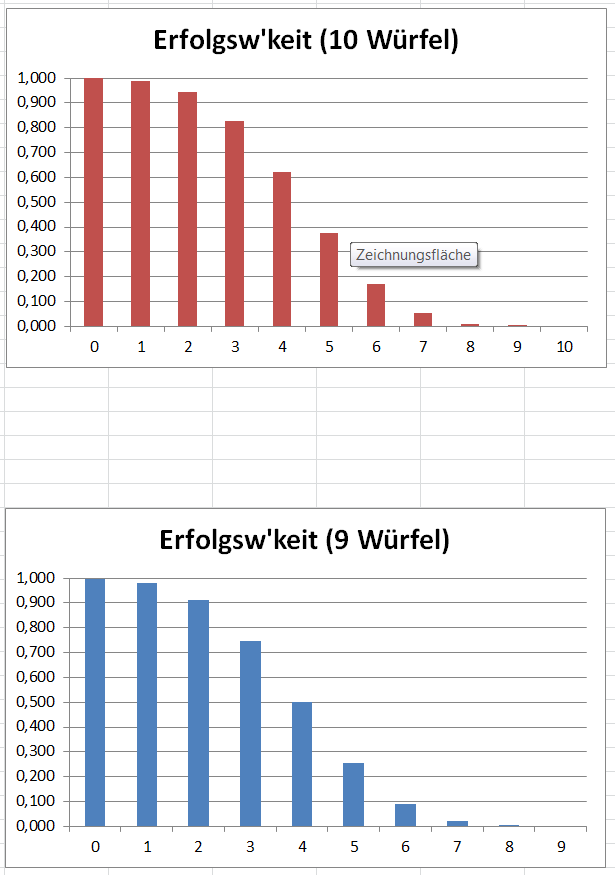
Die Zahl k der benötigten Erfolge ist hier auf der x-Achse, die Erfolgswahrscheinlichkeit auf der y-Achse.
Wie man sieht, ist die Erfolgswahrscheinlichkeit für nicht-automatische Erfolge (also alles mit k > n/2) echt kleiner als 1/2. Und genau das war ja mein Kritikpunkt: Die Regel für automatische Erfolge nimmt den Spielern die Erfolgserlebnisse und lässt ihnen nur die Würfe, die tendenziell eher scheitern. Was ich schade finde.
Wenn du die Mathematik dazu nochmal nachlesen magst: ich fand
dieses Tutorium ganz gut erklärt.
